Jump Game
Jump Game
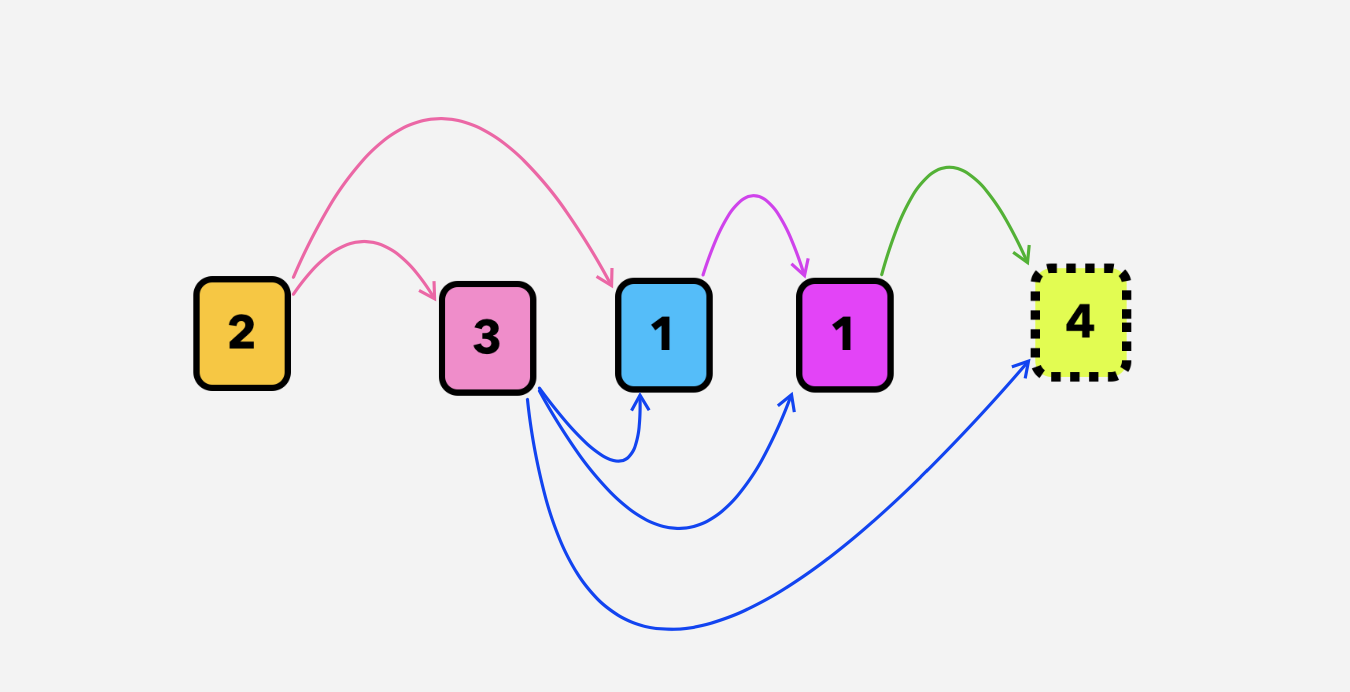
Problem: Given an array of non-negative integers nums, you are initially positioned at the first index of the array. Each element in the array represents your maximum jump length at that position. Your goal is to reach the last index in the minimum number of jumps. You can assume that you can always reach the last index.
Let’s look at two different approaches:
1. Recursive [without memoization]
Basically checking for possible range on each element.
possible_jumps = { curr + [1..nums[idx]] }
Basically, we are checking for all possible options.
Range space is: [1..nums[idx]], jump space will be: idx + [1..nums[idx]]
def solve(nums):
import math
def recurse(idx):
if idx == len(nums) - 1:
return 0
if idx >= len(nums):
return math.inf # not possible, it is beyond the n'th element
res = math.inf
val = nums[idx] # we will check for all possible jumps, range: [1..nums[idx]] (inclusive)
for v in range(1, val + 1):
res = min(res, 1 + recurse(idx + v))
return res
return recurse(0)
2. Dynamic Programming [Bottom Up], Push DP
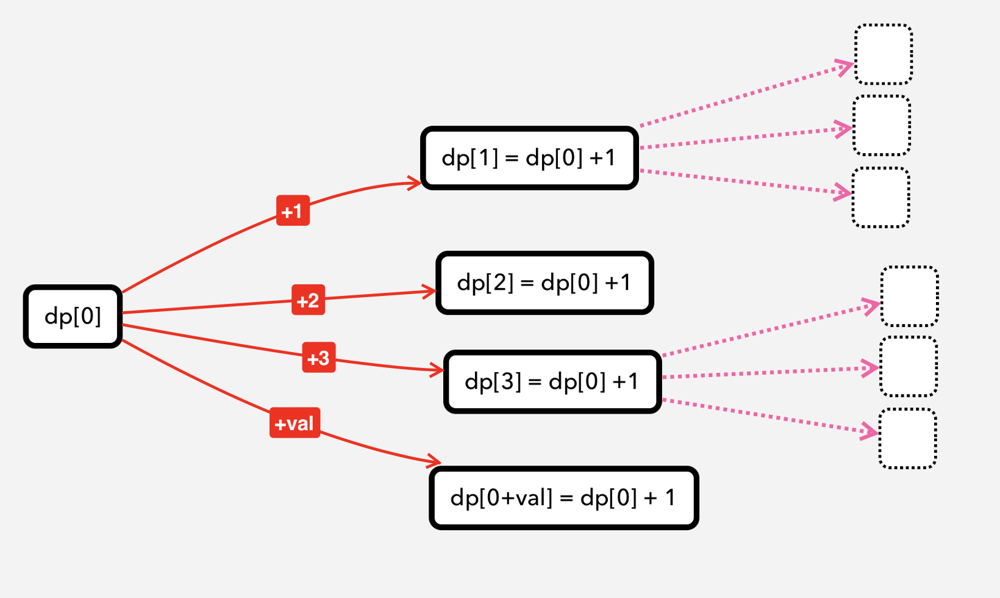
For DP State Relations, take a look into the following picture:
Base state for dp[0] will be 0, because cost of reaching to idx=0 is ZERO.
class Solution:
def jump(self, nums: List[int]) -> int:
return self.dpsolve(nums)
def dpsolve(self, nums):
import math
n = len(nums)
dp = [math.inf] * n
dp[0] = 0
for i in range(0, n):
for v in range(1, nums[i]+1):
if i + v < n:
dp[i+v] = min(dp[i]+1, dp[i+v])
return dp[n-1]
![Floyd-Warshall [SSSP]](../images/graph/floyd/cover.png)