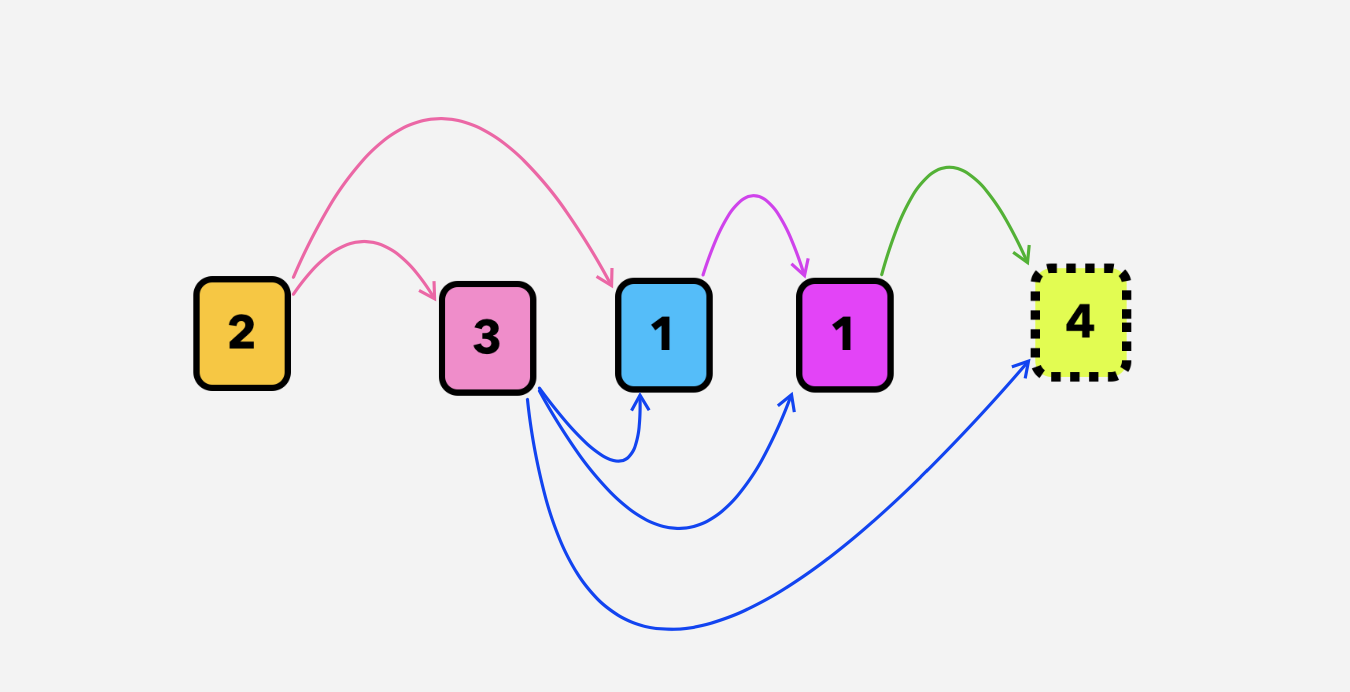
Permutation Sequence

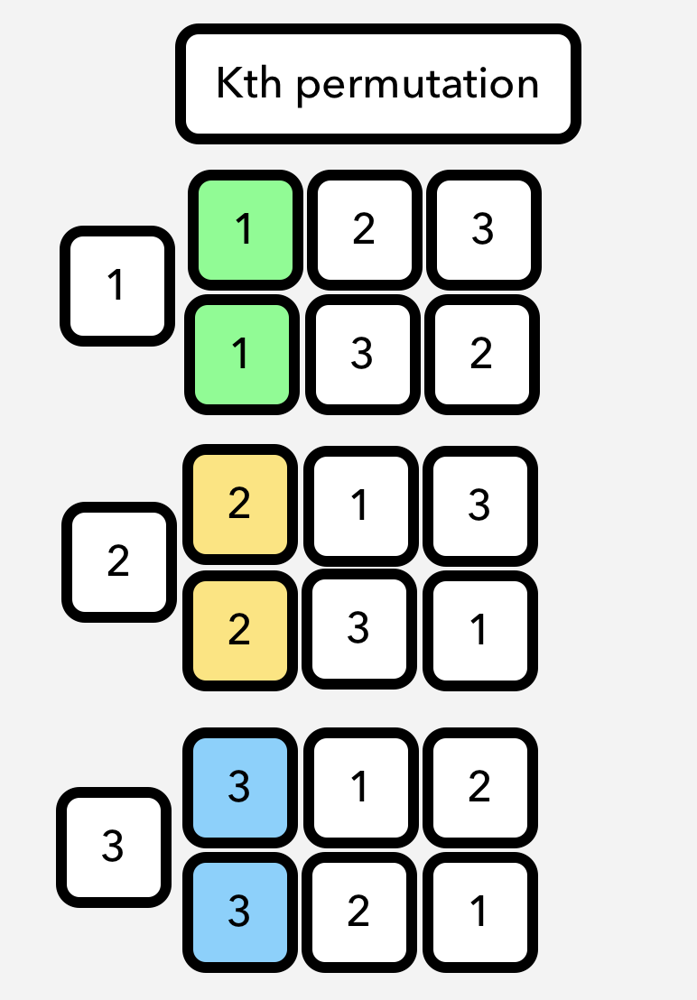
Problem: The set [1, 2, 3, …, n] contains a total of n! unique permutations. Given n and k, return the kth permutation sequence.

This problem is really cool and helpful to gain intuition on permutation problems. Both recursive and iterative approaches are actually similar, but I will explain recursive approach, because it’s much more native way for this problem. Core idea here is: think the problem recursively as,

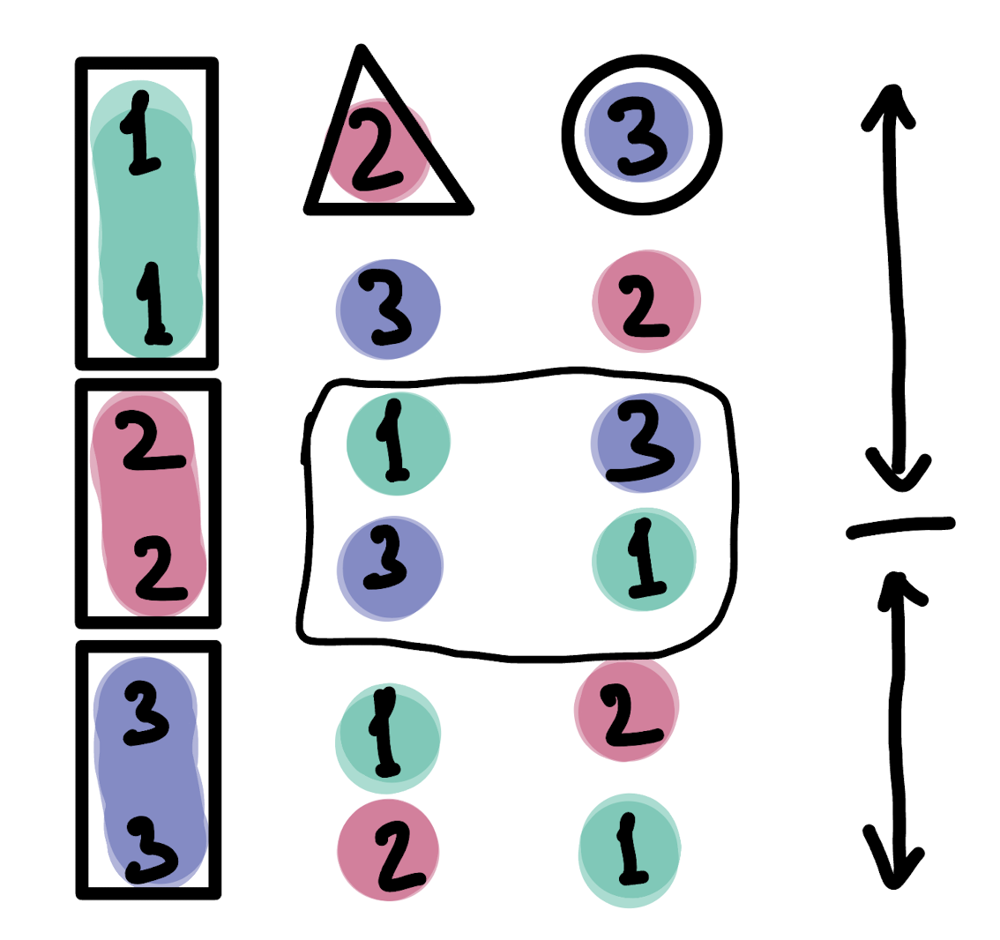
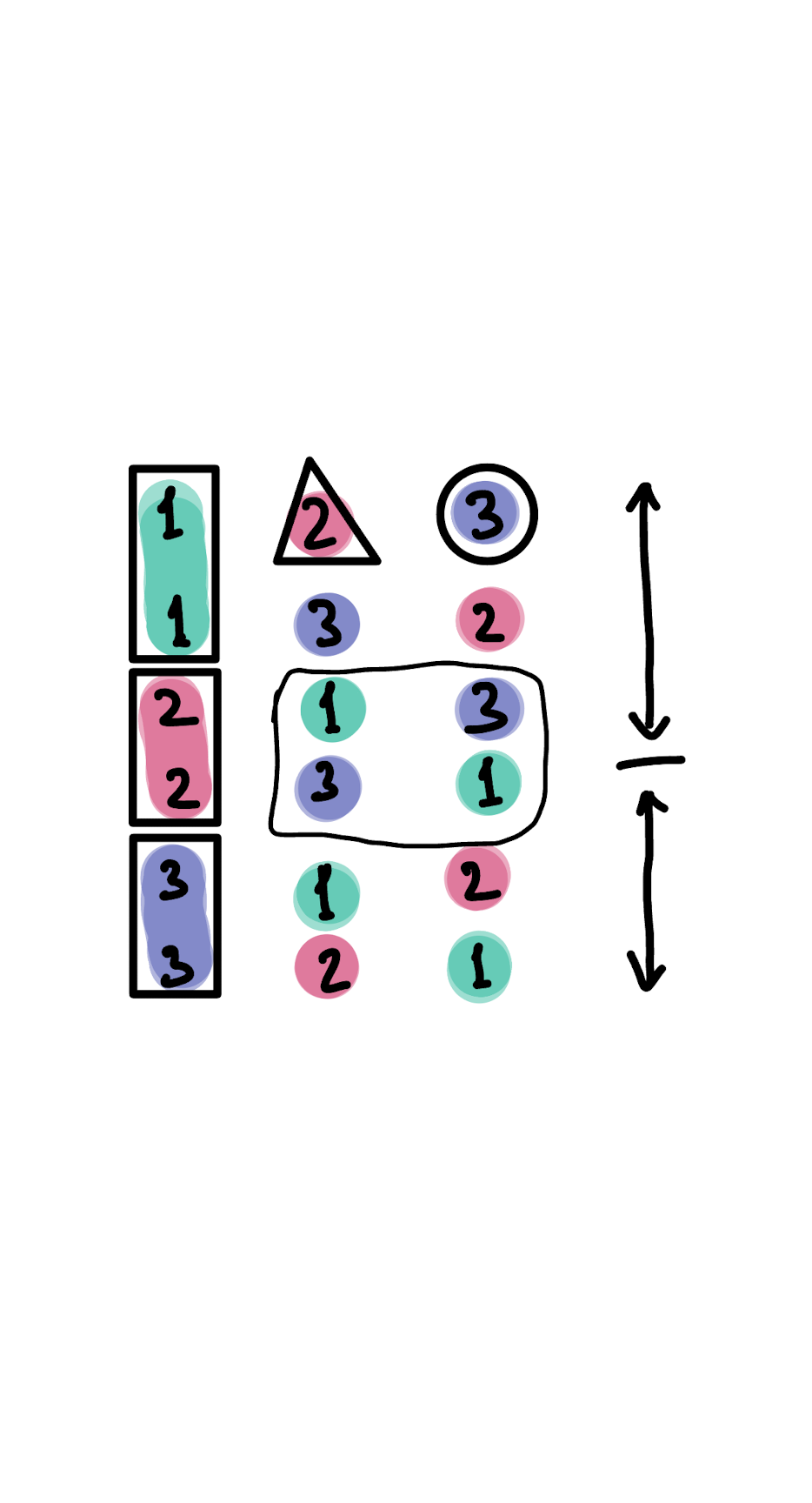
Proof: Initially for the first index of number, there are n! options. K initially resides in [1…K…N!] range. But for each number, there is block_size. What is this block size? Block size is it’s (for each number) total number of contributions on current index to the permutations. Initially there are n numbers available as a choice. For next id there are n-1, for next after next there are n-2 etc.. You can think about that as a pigeon-hole principle.

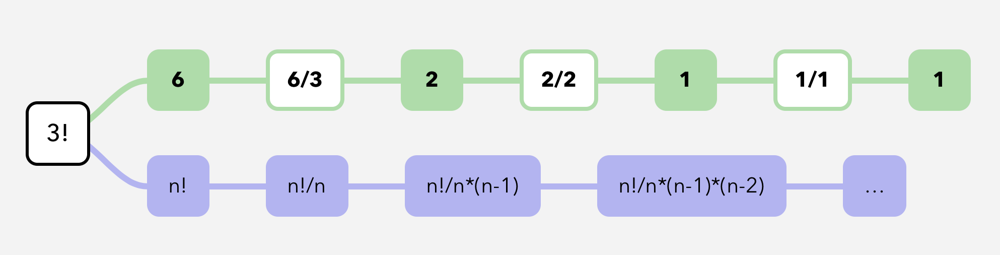
0. For the 0th state: n! is the initial block size [this state is abstact]
1. For the first index: prev_block_size / n -> n!/n
2. For the second index: prev_block_size / n-1 -> n!/n*(n-1)
3. For the third index: prev_block_size/(n-2) -> n! / n * (n-1) * (n-2)
…

To find k, n, block_size for the next recursive state?

1. new k will be k % curr_block_size (you can clearly see it from the pictures above). new k for the next recursive part will reside within borders of the previous block.
2. next n will be, n-1. will also delete n from the selection space.
3. new block_size will be, previous_block_size / new_space

class Solution:
    def getPermutation(self, n: int, k: int) -> str:
        return self.solve(n, k)

    def solve(self, n, k):
        '''
            123
            132

            213
            231

            312
            321

            how many permutations?
            n * (n-1) * (n-2) [main range]

            main range: 1...n!
            main blocksize: n!//n (for example: 3 numbers, 3! permutations, 3!//3 block size)
            main formula: block_size * numbers = permutationsize

            second range: 1...(n-1)!
            second blocksize:
            second formula: block_size * (n-1) = (n-1)!


            K ?

            1.... K .... n!

            (k // block_size + 1) -> number
            k % block_size -> new_k (for remaining partition)
            initial_block_size = n!

            [2,3,1]

        '''
        import math

        nums = [i for i in range(1, n+1)]

        def recurse(n, k, block_size, res):
            if n == 0:
                return res

            block_size = block_size // n
            numidx = k // block_size
            res += str(nums[numidx])
            del nums[numidx]
            return recurse(n-1, k % block_size, block_size, res)

        return recurse(n, k-1, math.factorial(n), '')

Further Research

• Make research about the factorial number system