Manacher's Algorithm

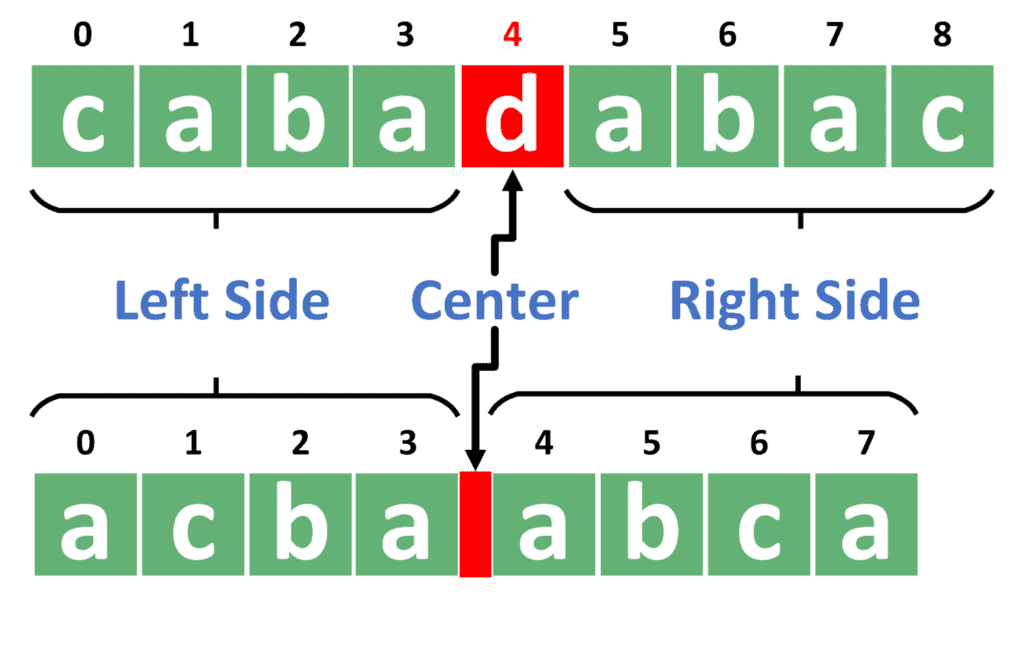
There are multiple different ways of implementation for this problem, like DP(lcs, etc), expanding from center. But the most optimal approach is Manacher’s Algorithm, time complexity: O(n). It’s core idea is calculating current palindrome information based on previous calculated palindrome information. Let’s draw it and see some formulas and implications.

Some formulas & implications: To handle both even & odd lengths we need some preprocessing on string. It will be like this: ‘@#s#t#r#$’ There will be: n string chars + (n+1) ‘#’ symbol + 1 ‘@’ symbol + 1 ‘$’ symbol = 2n + 3 2n+3 => will be odd always

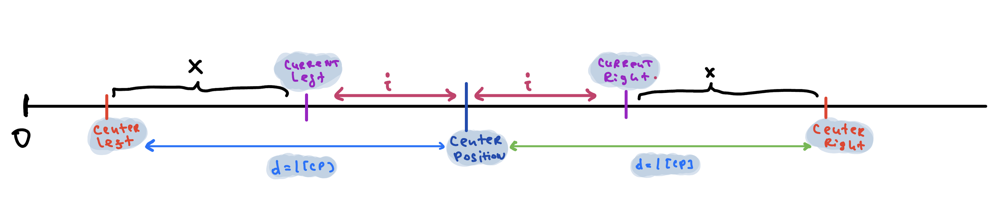
centerPos => is current center which expanded longer distance

1. centerLeft + d = centerPos
2. centerRight - d = centerPos
3. centerLeft + centerRight = 2*centerPos
4. centerLeft + x = currentLeft (or mirror of currentRight)
5. x = d - i = centerRight - i
6. centerLeft + centerRight - i = currentLeft

Important implication: currentLeft (mirror) = 2*centerPos - i

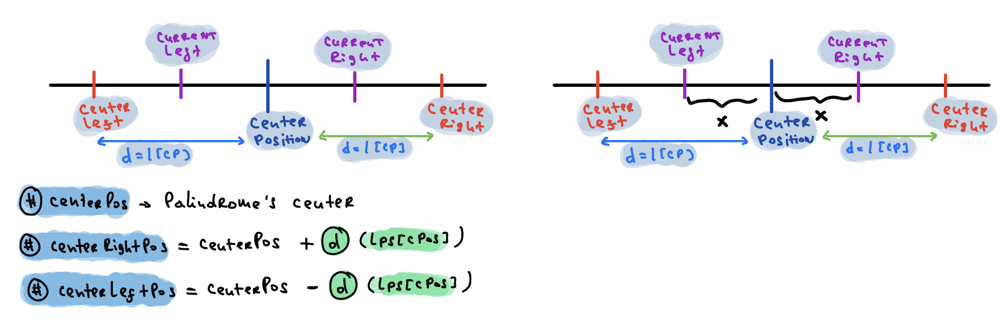
But there could be two different cases:

1. currentLeft - distance[currentLeft] > centerLeft [it means it’s within borders of the centerLeft…centerPosition]
2. currentLeft - distance[currentLeft] < centerLeft [it means it’s out of borders of the centerLeft..centerPosition]

For the second case, we don’t know about the out of border information, therefore we need to cut until the border. [centerRight-currentLeft]

    def manachersSolve(self, s: str) -> str:
        # processing str = @#s#a#l#a#m#$
        newlen = 2*len(s) + 3
        newstr = ['@']
        newstr += [f'#{c}' for c in s]
        newstr += ['#$']
        newstr = ''.join(newstr)
        p = [0] * newlen

        maxlen = 0
        centerPos = 0
        centerLeftPos = 0
        centerRightPos = 0

        # centerRightPos - d = centerPos
        # centerLeftPos + d = centerPos
        # centerRightPos + centerLeftPos = 2*centerPos
        # if centerPos + p[centerPos] > centerPos + i [inside]
        # if centerPos + p[centerPos] < centerPos + i [outside]
        # if centerPos - p[centerPos] < centerPos - i [inside]
        # if centerPos - p[centerPos] > centerPos - i [outside]

        for i in range(1, newlen-1):
            if i < centerRightPos:
                p[i] = min(centerRightPos-i, p[2*centerPos - i])

            while (newstr[i-p[i]-1] == newstr[i + p[i] + 1]):
                p[i] += 1

            if (i + p[i] > centerRightPos):
                centerPos = i
                centerRightPos = centerPos + p[i]

            if p[i] > maxlen:
                start = (i-p[i]-1)//2
                maxlen = p[i]

        return s[start:start+maxlen]