Convert to ZigZag
Convert to ZigZag
Problem: Print the string “SALAM” in a zigzag pattern on a given number of rows.
I will try to explain my approach, don’t know if someone tried to solve in this way. There are four key observations here:
Observation#1:
If number of rows is equal to or greater than length of the string, string will not jump to other columns (not enough string to spread other columns).
If number of rows is equal to 1, the same thing.
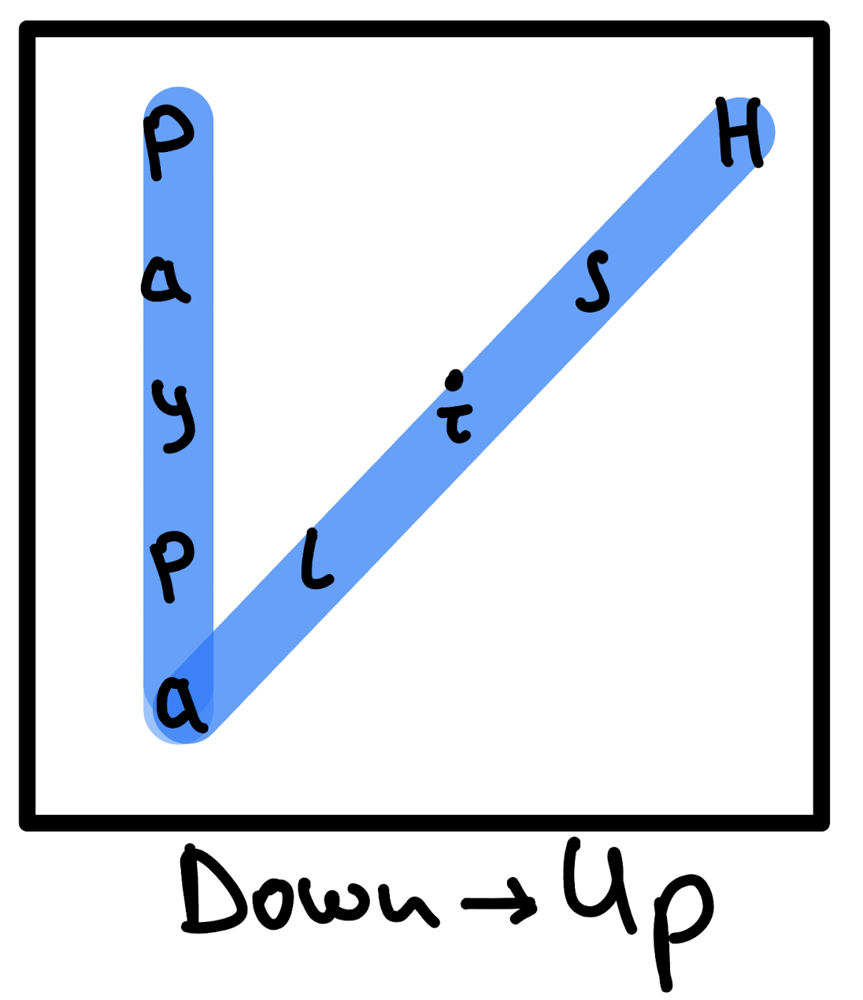
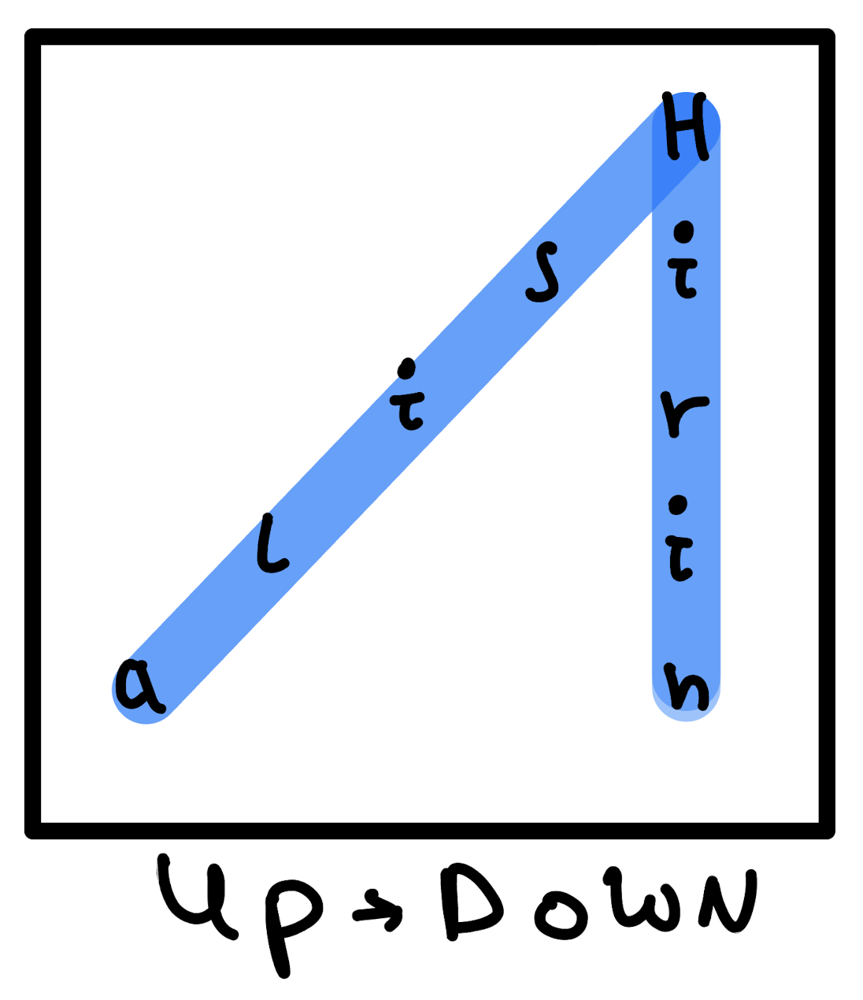
Observation#2:
We can see two different waves. Down->Up, Up->Down
They are changing on each iteration.
We can visualize these waves as following:


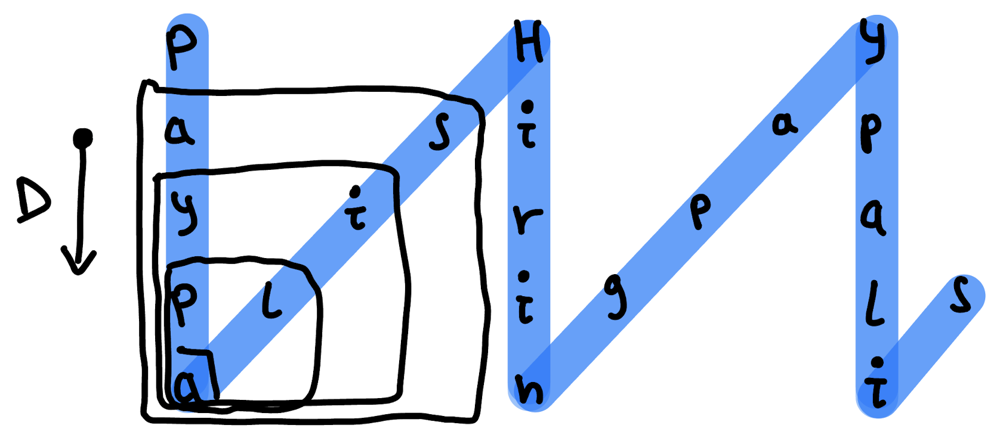
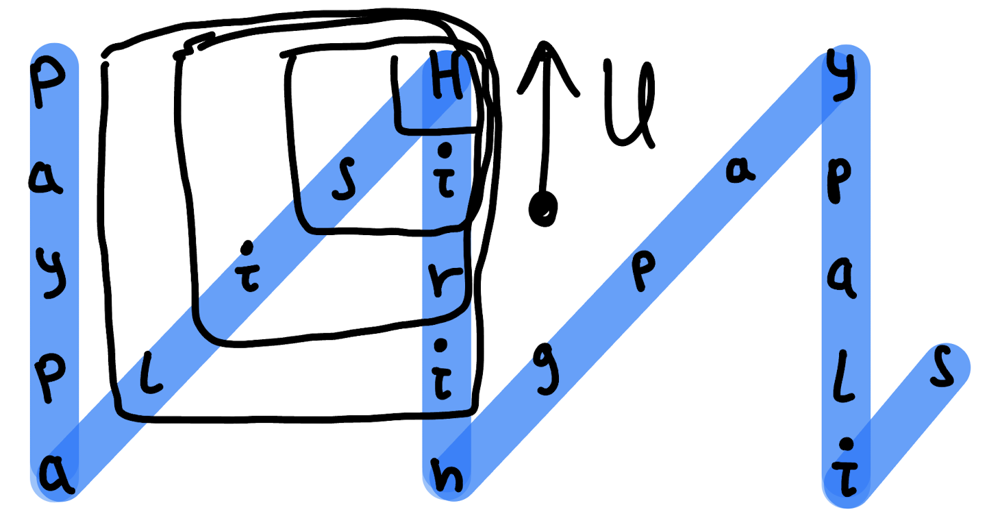
Observation#3:
We can think about parallel columns as a square. As we can see, distance between parallel column chars is:
For Down->Up: distance = heightOfSquare + diagonalOfSquare = (m-i) + (m-i) (i is 1 based index)
For Up->Down: distance = diagonalOfSquare + heightOfSquare = (i-1) + (i-1) (i is 1 based index)
Let’s draw it.
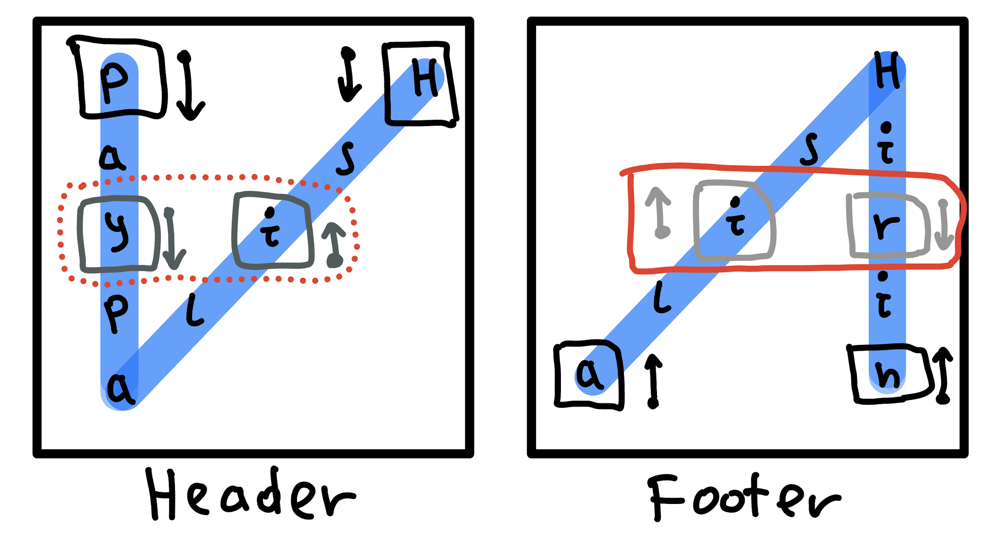
Observation#4: If you take attention to header and footer points of waves, their direction is not changing, remains the same on each iteration. Reason? because it completes one full PERIOD, and doesn’t change it’s direction. (it’s similar to the physic’s wave funcions :) )
By considering these observations, let’s implement:
def convert(self, s: str, numRows: int) -> str:
ans = ''
n = len(s)
m = numRows
if (m==1) or (n <= m):
return s
for i in range(1, m+1):
direction = 0 # starting with Down
startIdx = i-1
ans += s[startIdx]
while (startIdx < n):
if i == 1:
direction = 0 # set direction to down (header's direction is always down)
elif i == m:
direction = 1 # set direction to up (footer's direction is always up)
if not direction:
stepsize = 2*(m-i) # heightOfSquare + diagonalOfSquare = (m-i) + (m-i)
else:
stepsize = 2*(i-1) # diagonalOfSquare + heightOfSquare = (i-1) + (i-1)
nextIdx = startIdx + stepsize # update next possible position
startIdx = nextIdx # next start position will be current next position
if nextIdx < n: # if there is char in nextIdx add it to the result
ans += s[startIdx]
direction ^= 1
return ans