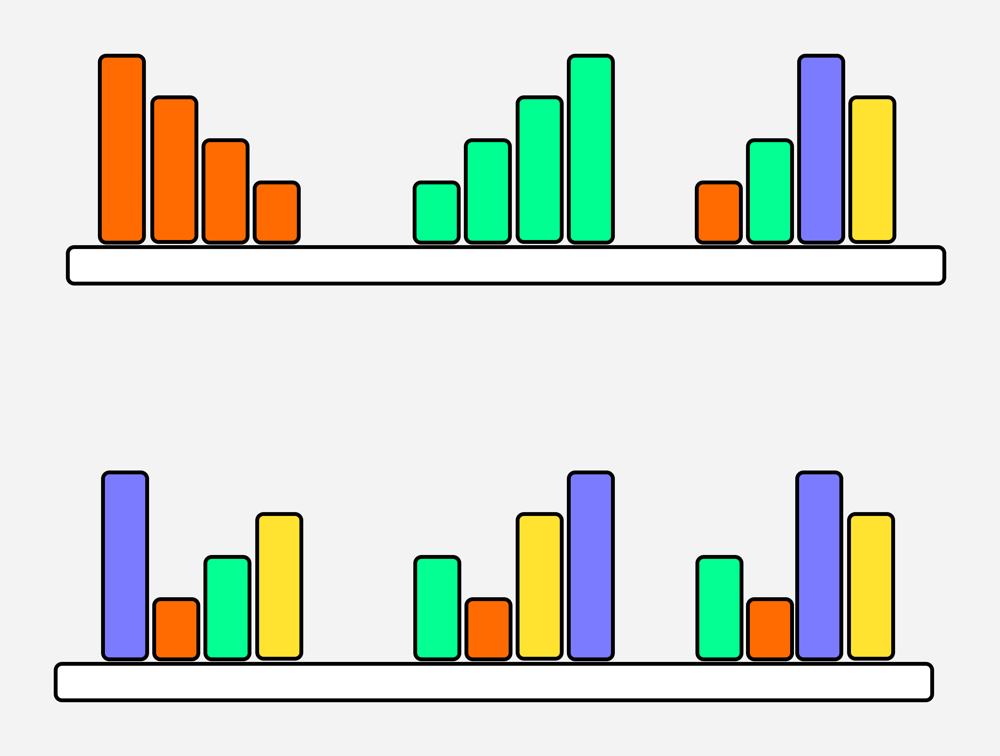
The Skyline Problem

The Skyline (2D Interval merging)

Question is: A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively. The geometric information of each building is given in the array buildings where buildings[i] = [lefti, righti, heighti]:
lefti is the x coordinate of the left edge of the ith building.
righti is the x coordinate of the right edge of the ith building.
heighti is the height of the ith building.
You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0. The skyline should be represented as a list of “key points” sorted by their x-coordinate in the form [[x1,y1],[x2,y2],…]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline’s termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline’s contour.

Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, […,[2 3],[4 5],[7 5],[11 5],[12 7],…] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: […,[2 3],[4 5],[12 7],…]

Approximately it took 2-3 days to write this explanation. All visualization belongs to me. Article might be challenging to digest at the first attempt, therefore divided into 2 parts. For the next part, will include : 1D Fenwick tree, 2D Fenwick Tree and Segment Tree implementations of this problem.

Let’s start from the beginning, how can we approach this problem?
What is the input data? Input data is: (startX, endX, height), actually we can express height as endY-startY, startY is always ZERO, so we can write endY as height.
Input data: (startX, endX, height)
Can we combine them into the 1D data structure? Let’s try.
For every cell between [startX and endX) map OY data into OX data. We can call it heightmap.
map[startX] = y1
map[x2] = y1
map[x..] = y1
map[endX-1] = y1
It will look like as following:

Let’s take a closer look into the implementation:

Pseudo-code:
for each rectangle in rectangles:
	for each x-coordinate along Ox axis:
	check for :
		Is x-coordinate within rectangle's borders?
			If yes: existing map[x1] is greater that current rectangle's height(or oY coordinate)?
			If yes: UPDATE map[x1] = height (Y)

Implementation:
def solve(self, buildings):
	maxx = max([end for _, end, _ in buildings])
	heightmap = [0] * (maxx+1)

for start, end, height in buildings:
	for i in range(start, end):
		# here we check for each rectangle(height) separately, for each start and end
		# we need to optimize redundant checks here
		# why redundant checks? 'cause, some intervals are intersected
		heightmap[i] = max(heightmap[i], height)

for idx, height in enumerate(heightmap):
	print(f'{idx} : {height}')

i = 0
result = []
while i <= maxx:
	curr = heightmap[i]
	start = i
	while i <= maxx and curr == heightmap[i]:
		i += 1
	result.append([start, curr])
return result

Can we optimize the running time? To optimize the problem, we need to track repetitive patterns in implementation. What can be redundant computation in our previous implementation?
for each start and end coordinates we repeated finding tallest rectangle - this is the key point.
Because the intervals alongside oX axis, can be in following states:

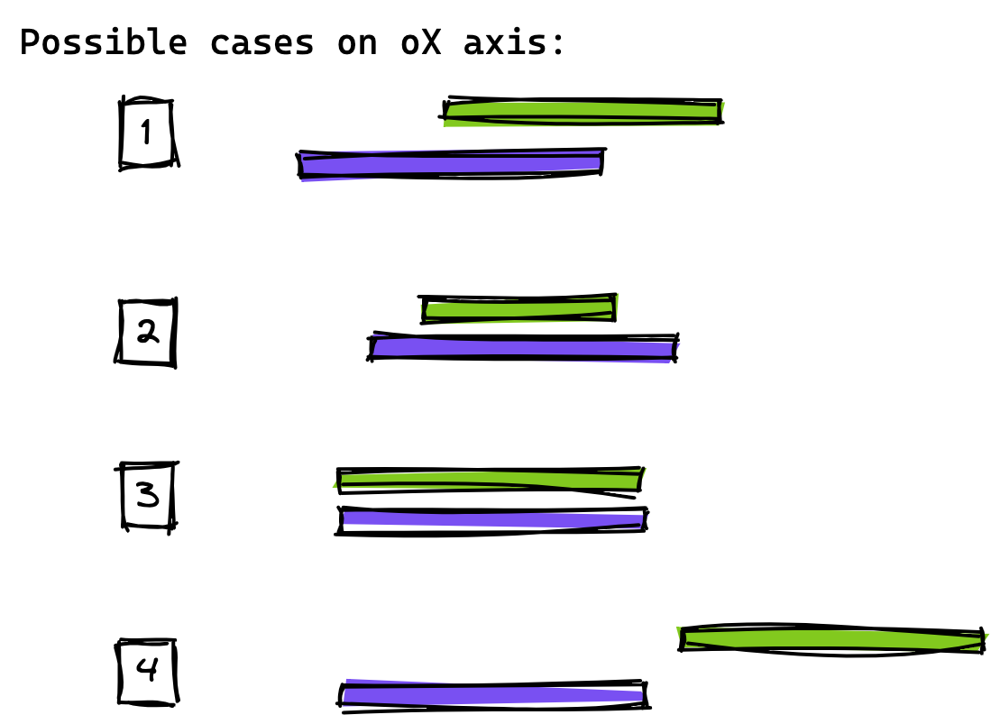
If we optimize redundant calculation of highest rectangle for that interval, we can optimize from O(n^2) to O(?). Idea is as following:
start from beginning of oX axis until end of oX axis:
dynamically maintain max rectangles alongside oX axis.

For dynamically maintaining (remove & add) heights and for query’ing max heights which data structures might be optimal for us?

• Fenwick Tree
• Segment Tree
• Heap (Priority Queue)

Let’s see two different Heap implementations. Core intuition behind this problem is:
when remove & add height to heap(or other data structures):

• check for previous has changed?
  
• YES -> append to result
  
• NO -> do nothing
  

Algorithm:

• sort start and end points according to this rule (for sequentially maintaining max height):
  
• for end points -> if e1==e2, sort heights from smaller to higher
  
• for start points -> if s1==s2, sort from higher to smaller
  
• identify the coordinate type? start or end
  
• if the coordinate type is start: add to heap (or other ds) and check if max has changed
  
• if the coordinate type is end: remove from heap (or other ds) and check if max has changed - if the max has changed: add it to ans [x, h]
  

• if the max has not changed: do nothing
  

• if s1==s2, add it which one is higher
  
• if e1==s2, add s2 first, then remove e2
  
• if e1==e2, remove e1 first, then e2
  

Implementation v1:

def solveV1(self, buildings):
	import heapq
	from functools import cmp_to_key

	def cmp(x, y):
		if x[0] != y[0]:
			return x[0] - y[0]
		elif x[0] == y[0]:
			return (-x[1] if x[2] == 'start' else x[1]) - (-y[1] if y[2] == 'start' else y[1])


	res = [[0, 0]]
	# heights_heap[0] - is the smallest element

	starts = [(start, height, 'start') for start, _, height in buildings]
	ends = [(end, height, 'end') for _, end, height in buildings]
	positions = starts + ends
	positions.sort(key=cmp_to_key(cmp))
	heights_heap = [0]

	for position, height, kind in positions:
		if kind == 'start':
			if height > -heights_heap[0]:
				res.append([position, height])
			heapq.heappush(heights_heap, -height)
		elif kind == 'end':
			old = heights_heap[0]
			heights_heap.remove(-height)
			heapq.heapify(heights_heap)
			if old != heights_heap[0]:
				res.append([position, -heights_heap[0]])
	return res[1:]

What are the critical points for us?

• Critical points are start and end points alongside oX axis. But they can have different conjunction cases. These different conjunctions and their behaviors are as followings:

Let’s see all different edge cases:
Case#1 (s2>s1, e2>e1):

Case#2 (s2>s1, e2=e1):

Case#3 (s2=s1, e2<e1):

Case#4 (s2>s1, e2<e1):

Case#5 (e1=s2, s2>s1):

ImplementationV2:

def solveoptimal(self, buildings):
	import heapq
	import math

	res = [[0, 0]]
	heights_heap = [(0, math.inf)]
	# heights_heap[0] - is the smallest element

	events = [(left, -height, right) for left, right, height in buildings]
	events += list(set([(right, 0, 0) for _, right, _ in buildings]))
	events.sort()

	for pos, height, right in events:
		# if curr pos >= positions in heap
		while heights_heap[0][1] <= pos:
			heapq.heappop(heights_heap)
		if height != 0:
			heapq.heappush(heights_heap, (height, right))
		if res[-1][1] != -heights_heap[0][0]:
			res += [[pos, -heights_heap[0][0]]]

	return res[1:]

Further Research

• Try to implement by using 1D Fenwick Tree
• Try to implement by using Segment Tree
• Try to implement by using 2D Fenwick Tree
• Can we propose a generalized solution to merge 3D intervals?